[알고리즘/정렬] Quick Sort 퀵 정렬 - C++ 코드, 시간/공간 복잡도

 

출처 : 위키백과

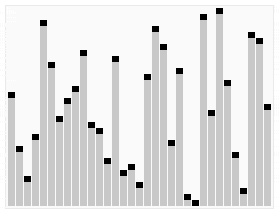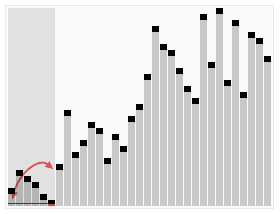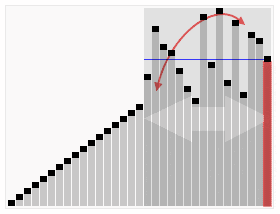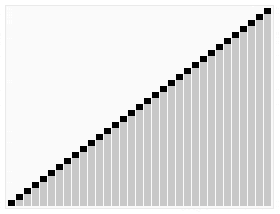
알고리즘에 대한 설명은 생략하고, 바로 코드로 넘어가겠다

void quickSort(vector<int>& v, int s, int e) {
	int pivot = v[s]; // 임의 선택
	int bs = s, be = e;

	while(s < e) {
		while(pivot < v[e] && s < e) e--;
		while(pivot > v[s] && s < e) s++;
		if(s > e) break;
		swap(v[s], v[e]);
	}

	if(bs < s) // 왼쪽
		quickSort(v, bs, s-1);
	if(be > e) // 오른쪽
		quickSort(v, s+1, be);
}

코드를 풀어서 설명하자면,

v[s] < pivot < v[e] 는 정상이다. 그 경우 s++, e--를 해야한다. (그냥 넘어가야 하니까)
그러다 정상이 아닌 곳에 도달하면 swap(v[s],v[e])를 한다.

그렇게 pivot 기준으로 작은 값은 왼쪽에, 큰 값은 오른쪽에 오도록 배치한 뒤에
pivot의 왼쪽에 대해서는 bs < s 인지 (범위 초과하지 않았는지) 확인하여 quickSort(v, bs, s-1);
pivot의 오른쪽에 대해서는 be > e 인지 (범위 초과하지 않았는지) 확인하여 quickSort(v, s+1, be);
를 하며 분할을 하기 시작한다.

재귀 호출이 한번 진행될 때마다 최소한 하나의 원소는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다

pivot 선택 방법

• 랜덤
• 3개를 랜덤으로 뽑아서 평균값 사용
• 세 값(좌측 끝, 중앙, 우측 끝)의 중위법을 이용하여 분할한다. 이 방법을 사용하면 중앙에서 분할될 가능성이 높아 전체적으로 정렬의 성능이 좋아진다.

여러 방법이 있으나 세번째 방법이 많은 라이브러리에서 사용된다.

 

시간 복잡도 : NlogN ~ N^2

Best	Avg	Worst
NlogN	NlogN	N^2

정렬된 배열에 Quick Sort를 수행하면 분할이 원소마다 모두 일어나게 되어 복잡도가 O(N^2)이 된다.
(pivot이 계속 최소값이거나 최대값인 경우)

하지만 보통의 경우 NlogN으로 나타나며, 현재 사용되는 정렬 알고리즘 중 일반적으로 가장 빠르다고 말할 수 있다.

빠른 이유는, 불필요한 데이터의 이동을 줄이고 먼 거리의 데이터를 교환할 뿐만 아니라, 한 번 결정된 피벗들이 추후 연산에서 제외되는 특성 때문이다.

안정성이 다소 부족하기 때문에, 2002년 Python을 시작으로 Tim Sort가 기본 라이브러리 정렬로 구현되기도 했다.

 

공간 복잡도 : O(logN)

최대 logN번 분할되기 때문에 그만큼 스택공간을 차지할 것이다.

이쯤에서 Worst 케이스라면 N번 분할되어 N^2의 시간복잡도가 되는데 왜 공간복잡도는 그대로지?!
할 수 있을텐데 (난 일단 그랬다)

놀랍게도 어떻게든.. logN만큼만 차지할 수 있다고 한다. 이와 관련된 글은 아래 두 링크에서 확인할  있다.

• https://stackoverflow.com/questions/12573330/why-does-quicksort-use-ologn-extra-space

• https://cs.stackexchange.com/questions/35509/can-anybody-explain-intuitively-why-quick-sort-need-logn-extra-space-and-merge

나는 아직 완벽하게 이해하지 못해서 일단 패스........ㅠ